使用Numpy生成随机数

使用Numpy生成随机数

　　Numpy 的随机模块，一套基于伪随机数生成的函数。随机是指逻辑上无法预测的事物。

np.random.seed()功能

　　在此示例中，您将模拟抛硬币。将使用函数np.random()，它绘制一个介于 0 和 1 之间的数字，使得该区间内的所有数字出现的可能性相同。如果您抽到的数字小于 0.5，即有 50% 的几率出现​​，则您说的是正面和反面。这种结果为真（正面）或假（反面）的结果称为伯努利试验。

　　伪随机数的工作原理是从一个称为种子的整数开始，然后连续生成数字。相同的种子给出相同的随机数序列，因此称为“伪”随机数生成。如果您想拥有可重现的代码，最好使用np.random.seed()函数为随机数生成器播种。

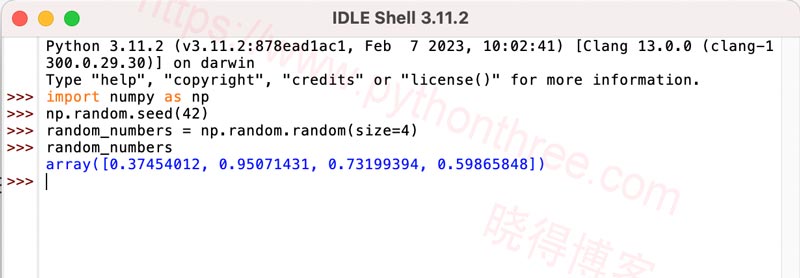
　　要进行抛硬币操作，您需要导入NumPy，为随机数生成器提供种子，然后抽取四个随机数。您可以使用关键字指定需要多少个随机数size。

import numpy as np
np.random.seed(42)
random_numbers = np.random.random(size=4)
random_numbers

输出：
array([0.3745012, 0.95071431, 0.73199394, 0.59865848])

　　你得到的第一个数字小于 0.5，所以它是正面，而剩下的三个是反面。您可以使用 less than 操作显式显示这一点，它为您提供一个包含布尔值的数组，头部为 True，尾部为 False。

heads = random_numbers < 0.5
heads

输出：
array([True, False, False, False], dtype=bool)

最后，您可以通过对布尔数组求和来计算正面的数量heads，因为在数值上下文中，Python 将 True 视为 1，将 False 视为 0。

np.sum(heads)

输出：
1

　　推荐：Python中使用Numpy创建含零的Numpy数组

模拟随机抛硬币

　　在下面的示例中，我们想知道如果我们一遍又一遍地重复抛硬币四次，出现四个正面的概率。我们可以用 for 循环来做到这一点。首先将计数初始化为零。然后我们重复 10,000 次重复四翻转试验。如果给定的试验有四个正面，我们会增加计数。

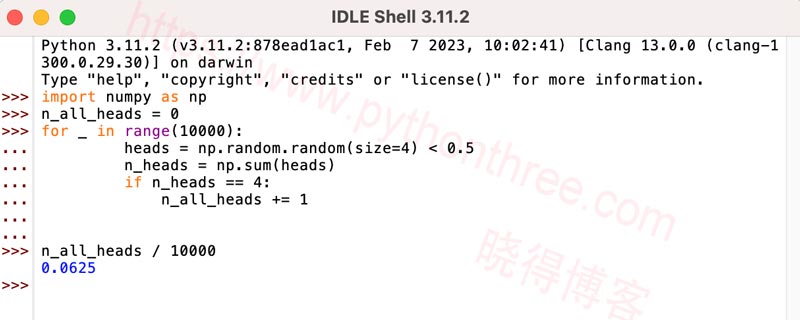
　　那么得到全部四个正面的概率是多少呢？它是所有正面​​朝上的次数除以试验总数。结果约为 0.06。

import numpy as np
n_all_heads = 0

# Initialize number of 4-heads trials
for _ in range(10000):
         heads = np.random.random(size=4) < 0.5
         n_heads = np.sum(heads)
         if n_heads == 4:
             n_all_heads += 1

n_all_heads / 10000

输出：
0.0621

　　推荐：NumPy数组操作

生成随机数的交互式

　　在此示例中，我们将生成大量介于 0 和 1 之间的随机数，然后绘制结果的直方图。如果数字真的是随机的，则直方图中的所有条形应该（接近）相同的高度，对于此示例，您将需要：

import numpy as np

np.random.seed(42)
random_numbers = np.empty(100000)
for i in range(100000):
    random_numbers[i] = np.random.random()

_ = plt.hist(random_numbers)
plt.show()

　　np.random.seed使用 seed为随机数生成器播种42。初始化一个包含 100,000 个条目的空数组 random_numbers 来存储random numbers. 确保你习惯np.empty(100000)这样做。编写一个for循环，使用 绘制 100,000 个随机数np.random.random()，并将它们存储在random_numbers数组中。为此，循环range(100000).绘制 的直方图random_numbers。在这种情况下没有必要标记轴，因为我们只是在检查随机数生成器。

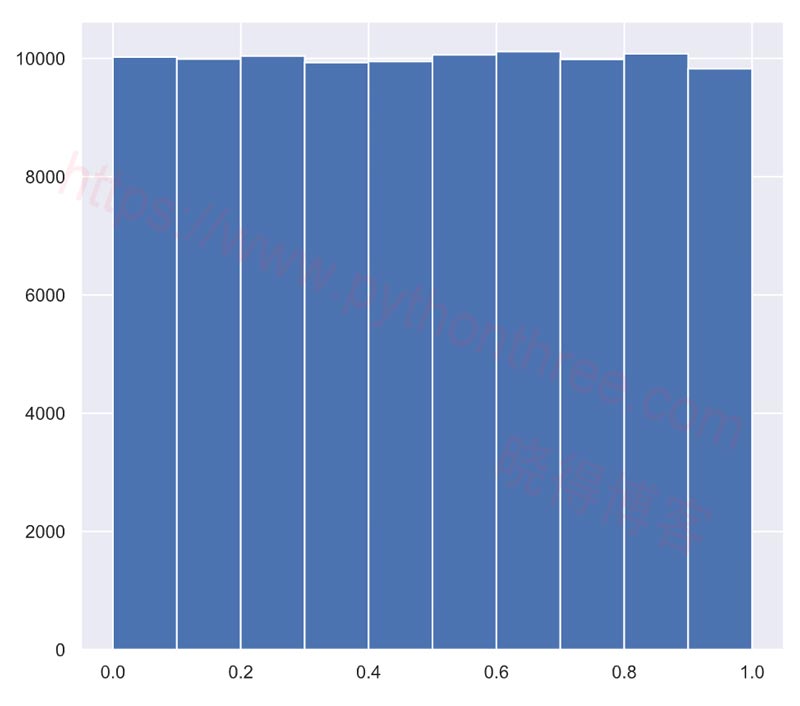
　　推荐：NumPy数值范围的数组

总结

　　以上是晓得博客为你介绍的使用Numpy生成随机数的全部内容，它是科学计算的基本包之一，NumPy 是您必须能够使用并且知道是否要使用 Python 进行数据科学的包之一，因为 NumPy 数组更紧凑，允许更快地访问读写项目，并且整体上更方便、更高效。

　　推荐：Numpy教程